数字ASIC设计概要：时序约束（Timing）简介

万物有序，唯有序而变化生，变化生而世界成。序者，规则也。

数字设计中，时序是最基本，也是最重要的概念。

基本概念

我们所说的数字设计多数时候都是指的同步逻辑。所谓同步逻辑，是说所有的时序逻辑都在时钟信号的控制下完成。这很像是大合唱，有很多的人参与，大家都根据同一个节拍来控制节奏，保持整齐。时钟信号就是那个节拍。其实很多地方都需要有一个节拍来协调系统的各个部分。比如工厂里的一条流水线。

流水线的每个工人从前一个人那里拿到中间产品，装配一个零件，然后交给下一个人；每一个人面前的空间只有放置一个中间产品的空间。装配一个零件并把中间产品交到下一个那里是需要时间的。如果这个时间太短，就会发生下一个人手中的零件还没装配好，新的中间产品又来了，却没处放的问题。如果这个时间太长了，就会发生下一个人闲着没事干的情况。前一种情况会导致流水线混乱，后一种情况则导致流水线的效率下降。因此，在确定的流水线效率要求下，我们就必须要求每位工人装配一个零件并把中间产品传到下一位工人的时间不能太快也不能太慢。这话也可以反过说，只有保证每位工人所用的时间在一个确定的时间范围内，我们才能保证流水线在按照特定的效率运行。

同步逻辑数字设计也好比是设计一个满足上述要求的“流水线”，只不过这个流水线是由传递二进制数据的数字器件组成。数据在两个存储单元之间传递，“效率”由时钟的周期(T)决定。每个存储单元在时钟节拍（通常是时钟信号的上升沿）的号令下工作。如同每个工人装配零件需要时间一样，每个存储单元正确地存储数据也是有要求的。它要求数据必须在时钟沿之前的某个时间就准备好（我们把这个时间称为 setup time，记为 t_setup），并且有这个数据必须保持不变一直到时钟沿之后的某个时间（我们把这个时间称为 hold time，记为 t_hold）才能完成数据的存储。 每个存储单元传递数据到下一个单元的时间我们记为 t_data，累比于上面流水线的例子，我们很容易得出，为了保证数据的正确传递，必须要求:

t_hold < t_data < T - t_setup

如果不是 t_hold < t_data，就会干扰下一个存储单元当前的数据存储；如果不是 t_data < T - t_setup，下一个存储单元就来不及存储下一个数据。实际中为了便于分析，这种约束关系也可以表示为：

t_slack-max = (T - t_setup) - t_data > 0
t_slack-min = t_data - t_hold > 0

这样一来，我们只需要检查每两个存储单元之间的 t_slack-max 和 t_slack-min 是否为正值就可以了。我们把这两个差值称为 Slack 。Slack 为正，我们称之为 "MET"，Slack 为负，我们称之为 Violation。

事实上，两个存储单元之间通常还会有组合逻辑单元，它们也传递数据，也对数据进行“加工”（二进制运算），只不过他们不需要理会时钟信号的存在，它们只是按照自己的能力大小（速度快慢）尽职而已。仍然以时钟节拍（比如时钟信号上升沿）做为参考的话，存储单元完成内部数据存储并输出到它的输出端（比如 Q 端口)也是需要时间的（我们记为 t_clk-q）。数据通过两个存储单元之间的组合逻辑所需要的时间记为 t_comb，则有:

t_data = t_clk-q + t_comb

至此，我们应该已经在体上知道了所谓的时序约束是指什么。但实际应用中，为了更好地将相关问题数学模型化，我们还需要进一步的概念定义。

Timing Path

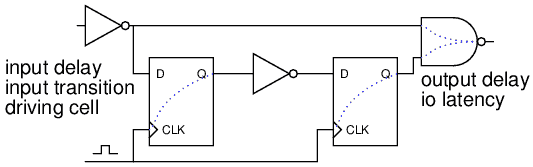
上面提到的 t_data 其实就是数据沿着一条数据通道传递所用的时间。而这条数据通道，我们就叫做 Timing Path。总结一个Design中可能的Timing Path，有下面四种：

• 从存储单元的时钟端口到另一个存储单元的数据输入端口的数据通道
• 从存储单元的时钟端口到 design 的输出端口
• 从 design 的输入端口到存储单元的数据输入端口
• 从 design 的输入端口到 design 的输出端口

有了 Timing Path 的定义，关于时序的计算事实上就可以描述为遍历 design 中所有的 Timing Path ，计算它们的 Slack。

• False Path : 所谓 False Path，简单来说就是指那些理论上存在，但实际上却不可能有数据沿它传输的 Timing Path。
• Disabled Timing Path : 人们有意识地排除掉的 Timing Path 。
• Multicycle Path : 通常的 Timing Path 在一个时钟周期内完成数据传输。有时，数据路径比较长，需要多于一个时钟周期才能完成数据传递，这种特殊的 Timing Path 叫做 Multicycle Path 。

时钟信号（Clock）

在上面的讨论中，我们所说的时钟信号都是理想情况下的。现实世界常常都是不会尽如人意的。
时钟信号传递到各个节点所用的时间不会总是相同的。时钟信号两个相邻的周期的波形也不会完全相同。

• Latency : 我们把时钟信号传递到存储单元的输入端所用的时间定义为 Clock Latency 。
• Uncertainty : 时钟信号传递到两个不同的节点所有的时间的差值我们称为 Clock Uncertainty。而 Uncertainly 事实上又可以分为两部分。
  • Skew : 同一个时钟信号由于传递路径不同导致的时间差异，我们称之为 Skew 。
  • Jitter (抖动) : 两个不同时刻（主要是相邻两个周期）的时钟信号由于时钟源本身的不稳定而产生的信号边沿的时间差异，我们称之为 Jitter。

t_uncertainty = t_skew + t_jitter

对于 Jitter, 通常都相对 Skew而言比较小， 我们也只能尽可能挑选稳定性好的时钟信号源。在实际设计中，我们更关心 Skew 多一些。我们常说的 CTS (Clock Tree Synthesis) 的主要目的就是如何让 Skew 尽可能地小。