判断点是否在多边形内(dot inside polygon)

判断点是否在多边形内的方法。

方法一：通过判断点在线段的同侧实现

基本原理

把多边形的每条边看作首尾相连的有向线段。
如果一个点相对于多边形的每条边（有向线段）的方向（左侧还是右侧）都相同，那么这个点就在这个多边形内部。

这种方法只适用于凸多边形，而不适用于凹多边形。

点在有向线段的哪一侧

定义有向线段(x1,y1),(x2,y2)，对于点(x,y)计算：

 v = (x2-x1)*(y-y1) - (y2-y1)*(x-x1)

v=0表示点在线段所在的直线上，v>0表示点在线段的左侧，v<0表示点在线段的右侧。

上面的计算式也可以表示比较斜率的大小：

  (y-y1)/(x-x1) > (y2-x1)/(x2-x1)

方法二：通过判断穿越点的线段数目来实现

这个方法来自 Point-In-Polygon Algorithm — Determining Whether A Point Is Inside A Complex Polygon。

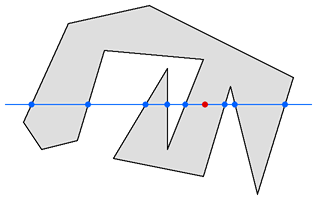
以要判断的点(x,y)的y坐标对应的水平直线作为参考，如果多边形的一条边穿过了这条参考线，则称作一个node。如果点(x,y)每边（左右）的node数目是奇数的话，那么可以判断这个点在多边形内部。

原文中的例程如下：

bool pointInPolygon() {

  int      i, j=polySides-1 ;
  boolean  oddNodes=NO      ;

  for (i=0; i<polySides; i++) {
    if ((polyY[i]< y && polyY[j]>=y
    ||   polyY[j]< y && polyY[i]>=y)
    &&  (polyX[i]<=x || polyX[j]<=x)) {
      oddNodes^=(polyX[i]+(y-polyY[i])/(polyY[j]-polyY[i])*(polyX[j]-polyX[i])<x); }
    j=i; }

  return oddNodes; 
}